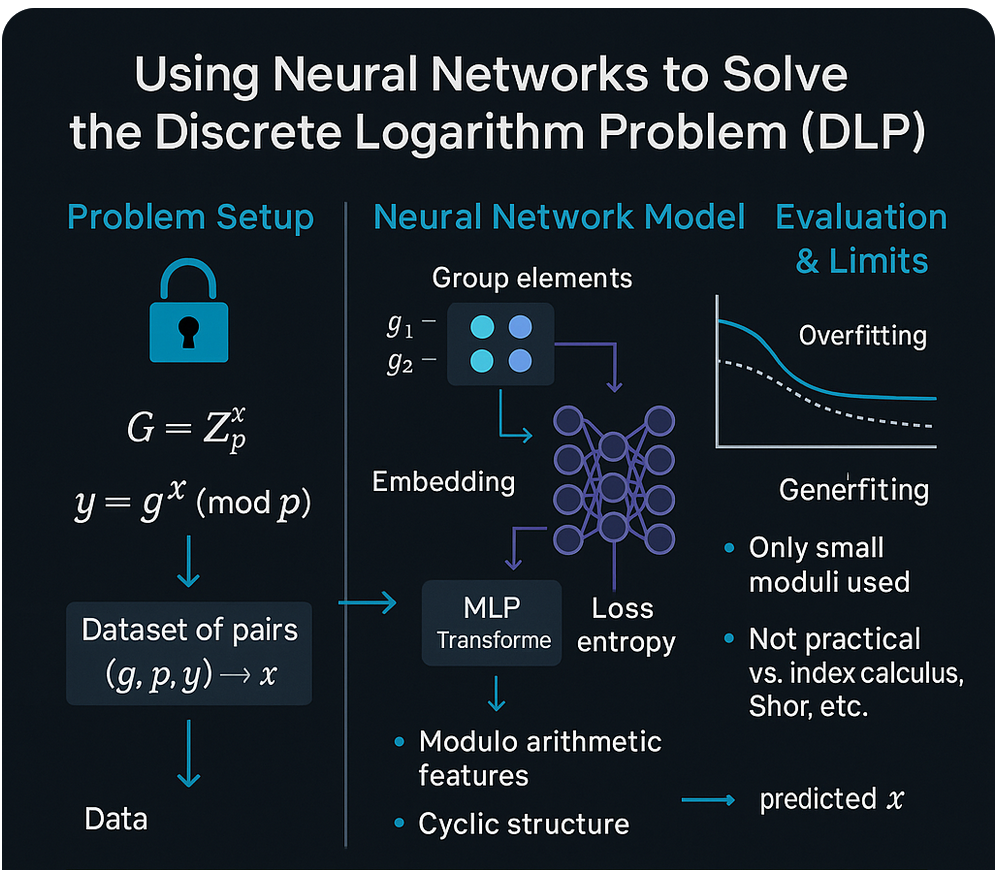
The aim is to investigate whether machine learning can help in finding patterns that might assist in solving the Discrete Logarithm Problem (DLP).
The Discrete Logarithm Problem underpins the security of ECDSA, widely used in Bitcoin. Given a public key Q = k·G, where G is the generator point, recovering the private key k is computationally infeasible with classical algorithms [1][2]
Previous Work
Previous research has established that, for uniformly random private keys, gradient-based machine learning methods are unable to reliably recover fixed bits of the secret from the public key coordinates alone [3]. This negative result closes off one direct approach, but it does not exhaust the possibilities for applying ML to the Discrete Logarithm Problem. In fact, several other avenues remain largely unexplored:
- Bucket or range ranking — Using ML to assign likelihood scores to different regions of the key space, enabling guided classical searches.
- Feature engineering beyond coordinates — Incorporating derived elliptic curve values as richer input features.
- Hybrid approaches — Combining ML ranking with algorithms like Baby-Step/Giant-Step or Pollard’s Rho to focus computation on high-probability zones.
These strategies suggest that while the direct mapping from Q = k·G to k may resist simple gradient descent, machine learning still offers multiple pathways to reduce the effective complexity of the DLP in practice.
Imminent Clash of ECDSA
Quantum computing poses a threat to the security of ECDSA due to Shor’s algorithm, which could solve the DLP efficiently. Transitioning to quantum-resistant cryptographic systems is increasingly urgent.[4]
Conclusions
Current machine learning techniques have not demonstrated the ability to break ECDSA when private keys are uniformly random, yet they remain a valuable tool in constrained or guided-search contexts. By integrating ML-driven heuristics with established cryptanalytic algorithms, it is possible to prioritize high-probability key regions and reduce the effective search space.
Future research should focus on:
- Hybrid ML–classical methods — Combining statistical scoring with algorithms such as Baby-Step/Giant-Step or Pollard’s Rho.
- Advanced feature engineering — Exploring representations beyond raw elliptic curve coordinates
- Quantum-era readiness — Evaluating how ML-guided approaches could complement post-quantum cryptanalytic techniques.
This dual perspective—respecting the theoretical hardness for ideal conditions, while exploiting practical weaknesses—keeps ML a relevant and evolving tool in the study of the Discrete Logarithm Problem.
References
[1] Menezes, A. J., Van Oorschot, P. C., & Vanstone, S. A. (1996). Handbook of Applied Cryptography. CRC Press.
[2] Koblitz, N. (1987). Elliptic curve cryptosystems. Mathematics of Computation, 48(177), 203–209.
[3] Takhanov, R., et al. (2023). Intractability of Learning the Discrete Logarithm with Gradient‑Based Methods. arXiv preprint arXiv:2310.01611. https://arxiv.org/abs/2310.01611
[4] Martin Roetteler, Michael Naehrig, Krysta M. Svore, and Kristin Lauter. Quantum Resource Estimates for Computing Elliptic Curve Discrete Logarithms https://www.microsoft.com/en-us/research/wp-content/uploads/2017/09/1706.06752.pdf